La regola di Titius-Bode (a volte chiamata semplicemente legge di Bode) è l'ipotesi che i corpi in alcuni sistemi orbitali, incluso il Sole, ruotino lungo semiassi a seconda della sequenza planetaria. La formula suggerisce che, estendendosi verso l'esterno, ogni pianeta sarà circa due volte più lontano dal Sole del precedente.
L'ipotesi prevedeva correttamente le orbite di Cerere (nella fascia degli asteroidi) e di Urano, ma non riuscì a determinare l'orbita di Nettuno e alla fine fu sostituita dalla teoria della formazione del sistema solare. Prende il nome da Johann Daniel Titius e Johann Elert Bode.

Origini
La prima menzione di una serie che si avvicina alla legge di Bode può essere trovata in Elements of Astronomy di David Gregory, pubblicato nel 1715. In essa dice: “… supponendo che la distanza dal Sole alla Terra sia divisa in dieci parti uguali, delle quali la distanza di Mercurio sarà di circa quattro, da Venere sette, da Marte quindici, da Giove cinquantadue, e da Saturno novantacinque . Un suggerimento simile, probabilmente ispirato da Gregorio, appare in un'opera pubblicata da Christian Wolff nel 1724.
Nel 1764, Charles Bonnet, nel suo libro Contemplation of Nature, disse: "Conosciamo i diciassette pianeti che compongono il nostro sistema solare [cioè i pianeti principali e i loro satelliti], ma non siamo sicuri che non ci sono più». A ciò Johann Daniel Titius, nella sua traduzione del 1766 dell'opera di Bonnet, aggiunse due suoi paragrafi in fondo a pagina 7 e in alto a pagina 8. Il nuovo paragrafo interpolato non si trova nel testo originale di Bonnet: né in italiano né traduzioni in inglese dell'opera.
Scoperta di Tizio
Ci sono due parti nel testo intercalato di Tizio. Il primo spiega la sequenza delle distanze planetarie dal Sole. Contiene anche alcune parole sulla distanza dal Sole a Giove. Ma questa non è la fine del testo.
Vale la pena dire qualche parola sulla formula della regola di Titius-Bode. Presta attenzione alle distanze tra i pianeti e scopri che quasi tutti sono separati l'uno dall' altro in una proporzione corrispondente alle loro dimensioni corporee. Dividi la distanza dal Sole a Saturno per 100 parti; poi Mercurio è separato da quattro di tali parti dal Sole; Venere - in 4 + 3=7 di queste parti; Terra - per 4+6=10; Marte - per 4+12=16.
Ma nota che da Marte a Giove c'è una deviazione da questa progressione così precisa. Uno spazio di 4+24=28 di tali parti segue da Marte, ma finora non è stato scoperto un solo pianeta. Ma il Signore Architetto dovrebbe lasciare questo posto vuoto? Mai. Cosìassumiamo che questo spazio appartenga senza dubbio alle lune di Marte ancora sconosciute, e aggiungiamo che forse Giove ha ancora intorno a sé alcune lune più piccole che non sono state ancora viste da nessun telescopio.

Rise of the Bode
Nel 1772, Johann Elert Bode, all'età di venticinque anni, completò la seconda edizione del suo compendio astronomico Anleitung zur Kenntniss des gestirnten Himmels ("Guida alla conoscenza del cielo stellato"), a cui aggiunta la seguente nota a piè di pagina, originariamente priva di fonte, ma annotata nelle versioni successive. Nelle memorie di Bode si può trovare un riferimento a Tizio con un chiaro riconoscimento della sua autorità.

Opinion Bode
Così suona la regola di Titius-Bode nella presentazione di quest'ultimo: se la distanza dal Sole a Saturno è assunta uguale a 100, allora Mercurio è separato dal Sole da quattro di queste parti. Venere - 4+3=7. Terra - 4+6=10. Marte - 4+12=16.
Ora c'è una lacuna in questa progressione ordinata. Dopo Marte segue uno spazio con un calcolo di 4+24=28, in cui non è stato ancora visto un solo pianeta. Possiamo credere che il Fondatore dell'universo abbia lasciato questo spazio vuoto? Ovviamente no. Da qui arriviamo alla distanza di Giove sotto forma di calcolo 4+48=52 e, infine, alla distanza di Saturno - 4+96=100.

Queste due affermazioni riguardanti tutte le tipologie specifiche e i raggi orbitali sembrano provenire da antichiastronomia. Molte di queste teorie risalgono a prima del diciassettesimo secolo.
Influenza
Tizio fu allievo del filosofo tedesco Christian Freiherr von Wolff (1679-1754). La seconda parte del testo inserito nell'opera di Bonnet è basata sull'opera di von Wolff del 1723, Vernünftige Gedanken von den Wirkungen der Natur.
La letteratura del XX secolo assegna la paternità della regola di Tizio-Bode a un filosofo tedesco. Se è così, Titius potrebbe imparare da lui. Un altro riferimento più antico fu scritto da James Gregory nel 1702 nella sua Astronomiae Physicae et geometryae Elementa, dove la sequenza delle distanze planetarie 4, 7, 10, 16, 52 e 100 divenne una progressione geometrica del rapporto 2.
Questa è la formula più vicina a Newton, ed è stata trovata anche negli scritti di Benjamin Martin e Thomas Ceard anni prima che il libro di Bonnet fosse pubblicato in Germania.
Ulteriori lavori e implicazioni pratiche
Tizio e Bode speravano che la legge portasse alla scoperta di nuovi pianeti, e infatti la scoperta di Urano e Cerere, la cui distanza concorda bene con la legge, contribuì alla sua accettazione da parte del mondo scientifico.
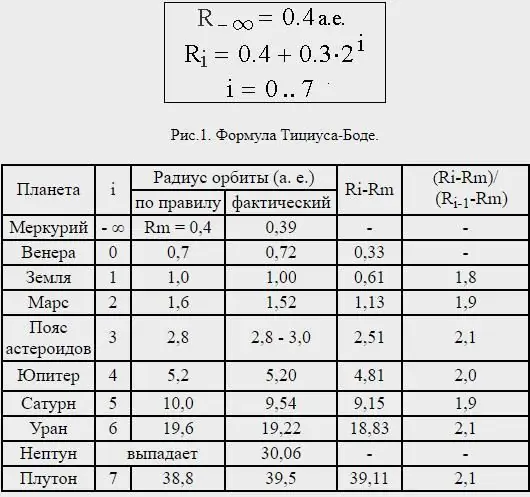
Tuttavia, la distanza di Nettuno era molto incoerente, e infatti Plutone - ora non considerato un pianeta - si trova a una distanza media che corrisponde grosso modo alla legge di Tizio-Bode prevista per il prossimo pianeta fuori Urano.
La legge originariamente pubblicata era approssimativamente soddisfatta da tutti i pianeti conosciuti - Mercurio e Saturno - con un divario traquarto e quinto pianeta. Questa è stata considerata una figura interessante, ma non di grande importanza fino alla scoperta di Urano nel 1781, che si inserisce nella serie.
Sulla base di questa scoperta, Bode ha chiesto la ricerca di un quinto pianeta. Cerere, l'oggetto più grande nella fascia degli asteroidi, fu trovato nella posizione prevista da Bode nel 1801. La legge di Bode fu ampiamente accettata fino a quando Nettuno fu scoperto nel 1846 e si dimostrò incompatibile con la legge.
Allo stesso tempo, un gran numero di asteroidi scoperti nella cintura ha superato Cerere dall'elenco dei pianeti. La legge di Bode fu discussa dall'astronomo e logico Charles Sanders Peirce nel 1898 come esempio di ragionamento fallace.

Sviluppo del problema
La scoperta di Plutone nel 1930 complicò ulteriormente il problema. Anche se non corrispondeva alla posizione prevista dalla legge di Bode, si trattava della posizione prevista dalla legge per Nettuno. Tuttavia, la successiva scoperta della cintura di Kuiper, e in particolare dell'oggetto Eris, che è più massiccio di Plutone ma non è conforme alla legge di Bode, screditò ulteriormente la formula.
Contributo di Serda
Il gesuita Thomas Cerda tenne il famoso corso di astronomia a Barcellona nel 1760 presso la Cattedra Reale di Matematica al Collegio di Sant Jaume de Cordelle (Seminario Imperiale e Reale dei Nobili di Cordell). Nel Tratado di Cerdas compaiono le distanze planetarie, ottenute applicando la terza legge di Keplero, con una precisione di 10-3.
Se prendiamo come 10 la distanza dalla Terra earrotondare per eccesso a un numero intero, è possibile esprimere la progressione geometrica [(Dn x 10) - 4] / [(Dn-1 x 10) - 4]=2, da n=2 a n=8. E utilizzando un movimento fittizio circolare uniforme all'anomalia di Keplero, i valori di Rn corrispondenti ai rapporti di ciascun pianeta possono essere ottenuti come rn=(Rn - R1) / (Rn-1 - R1), risultando in 1,82; 1, 84; 1, 86; 1.88 e 1.90, dove rn=2 - 0.02 (12 - n) è una relazione esplicita tra la continuità kepleriana e la legge di Tizio-Bode, che è considerata una coincidenza numerica casuale. Il risultato del calcolo è vicino a due, ma il due può benissimo essere considerato come un arrotondamento del numero 1, 82.

La velocità media del pianeta da n=1 a n=8 riduce la distanza dal Sole e differisce dal declino uniforme a n=2 per recuperare da n=7 (risonanza orbitale). Ciò influisce sulla distanza dal Sole a Giove. Tuttavia, anche la distanza tra tutti gli altri oggetti nel quadro della famigerata regola a cui è dedicato l'articolo è determinata da questa dinamica matematica.
Aspetto teorico
Non esiste una solida spiegazione teorica alla base della regola di Titius-Bode, ma è possibile che, data la combinazione di risonanza orbitale e mancanza di gradi di libertà, qualsiasi sistema planetario stabile abbia un' alta probabilità di ripetere il modello descritto in questa teoria dai due scienziati.
Poiché questa potrebbe essere una coincidenza matematica e non una "legge di natura", a volte viene chiamata regola piuttosto che "legge". Tuttavia, l'astrofisico Alan Boss sostiene che questo è semplicementecoincidenza, e la rivista di scienze planetarie Icarus non accetta più articoli che tentano di fornire versioni migliorate della "legge".
Risonanza orbitale
La risonanza orbitale dei principali corpi orbitanti crea regioni intorno al Sole che non hanno orbite stabili a lungo termine. I risultati della simulazione della formazione dei pianeti supportano l'idea che un sistema planetario stabile scelto casualmente possa soddisfare la regola di Titius-Bode.

Dubrulle e Graner
Dubrulle e Graner hanno mostrato che le regole di distanza della legge di potenza possono essere una conseguenza di modelli di nubi collassanti di sistemi planetari che hanno due simmetrie: invarianza rotazionale (la nuvola e il suo contenuto sono assisimmetrici) e invarianza di scala (la nuvola e il suo contenuto ha lo stesso aspetto su tutte le scale).
Quest'ultimo è una caratteristica di molti fenomeni che si pensa svolgano un ruolo nella formazione dei pianeti, come la turbolenza. La distanza dal Sole ai pianeti del sistema solare, proposta da Titius e Bode, non è stata rivista nell'ambito degli studi di Dubrulle e Graner.






