Quando si studia in fisica il movimento meccanico dei corpi nello spazio, si tiene sempre conto dell'accelerazione risultante. Consideriamo nell'articolo cos'è l'accelerazione e come viene indicata in fisica e risolviamo anche un semplice problema per calcolare questo valore.
Cos'è l'accelerazione e quali sono i suoi tipi?
Sotto l'accelerazione comprendi il valore, il cui significato è la velocità di variazione della velocità del corpo. Matematicamente, questa definizione è scritta come segue:
a=dv/dt.
Se si conosce la funzione tempo della velocità, basta trovare la sua derivata prima per calcolare l'accelerazione in un dato momento.
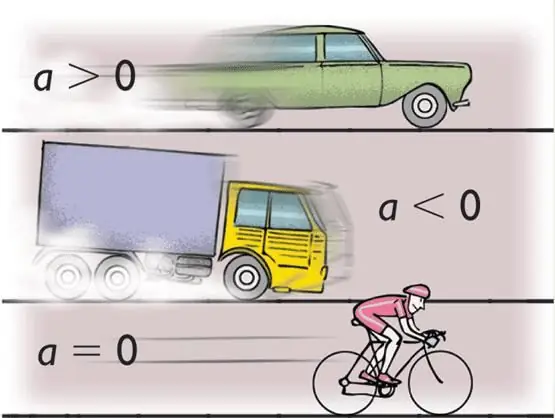
In fisica, la lettera di accelerazione è la a minuscola latina. Tuttavia, questa è la cosiddetta accelerazione lineare, che viene misurata in unità di m/s2. Oltre a ciò, c'è anche l'accelerazione angolare. Mostra la variazione della velocità angolare ed è espressa in unità di rad/s2. Questo tipo di accelerazione è indicato dalla lettera minuscola greca α (alfa). Qualche voltala lettera ε (epsilon) è usata per denotarlo.
Se il corpo si muove lungo una traiettoria curva, l'accelerazione totale viene scomposta in due componenti: tangenziale (che determina la variazione di velocità in magnitudine) e normale (che determina la variazione di velocità in direzione). Questi tipi di accelerazione sono indicati anche dalle lettere a, ma utilizzando gli indici corrispondenti: at e a. Normale è spesso chiamato centripeto e tangenziale è spesso chiamato tangente.
Infine, c'è un altro tipo di accelerazione che si verifica quando i corpi cadono liberamente nel campo gravitazionale del pianeta. È indicato dalla lettera g.
Problema in fisica per l'accelerazione
È noto che il corpo si muove in linea retta. La sua velocità nel tempo è determinata dalla seguente legge:
v=2t2-t+4.
E' necessario calcolare l'accelerazione che il corpo avrà al tempo t=2,5 secondi.
Seguendo la definizione di a, otteniamo:
a=dv/dt=4t - 1.
Ovvero, il valore a dipende linearmente dal tempo. È curioso notare che al momento iniziale (t=0) l'accelerazione era negativa, cioè diretta contro il vettore velocità. Otteniamo la risposta al problema sostituendo t=2,5 secondi in questa equazione: a=9 m/s2.






